https://www.acmicpc.net/problem/2632
2632번: 피자판매
첫 번째 줄에는 손님이 구매하고자 하는 피자크기를 나타내는 2,000,000 이하의 자연수가 주어진다. 두 번째 줄에는 A, B 피자의 피자조각의 개수를 나타내 는 정수 m, n 이 차례로 주어진다 (3 ≤ m, n
www.acmicpc.net
문제
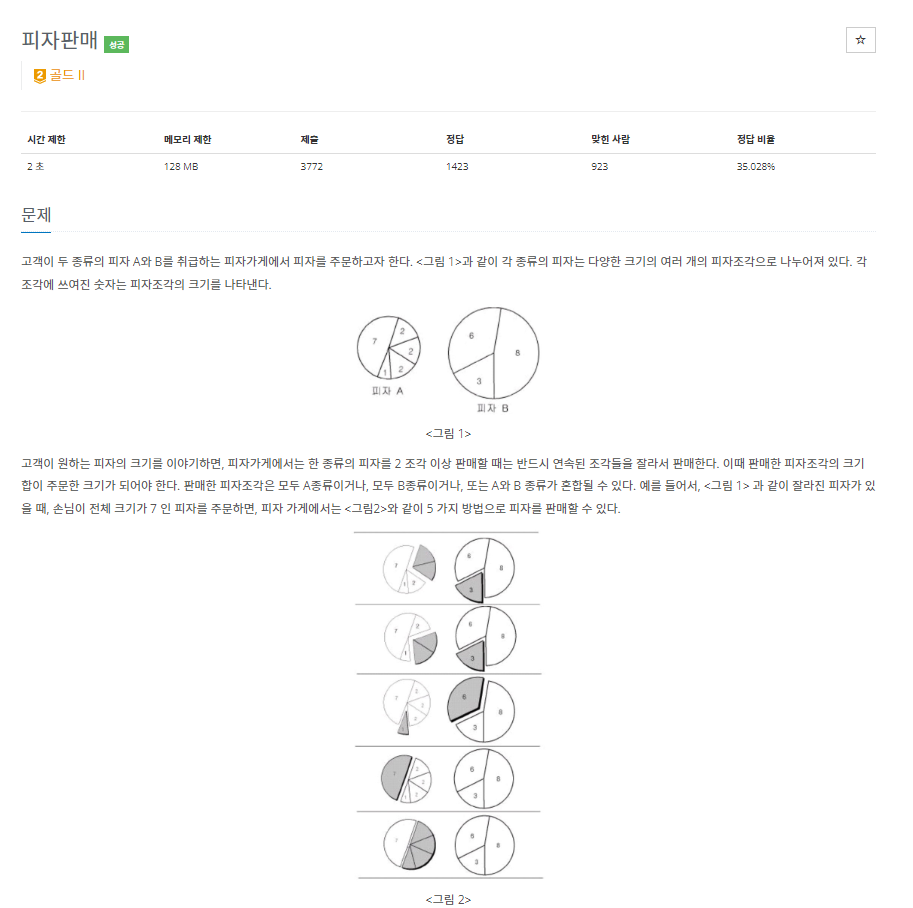
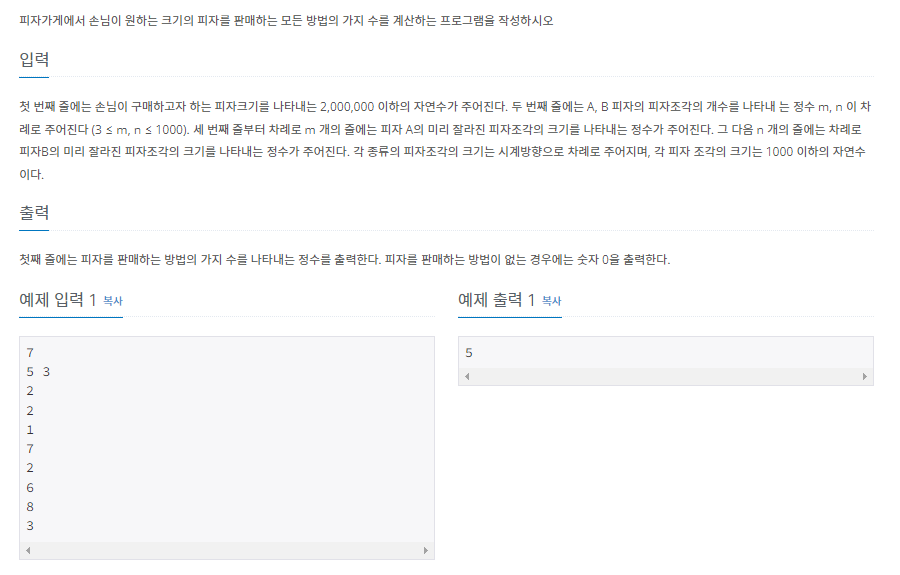
이해
나는 이 문제를 어떻게 이분탐색으로 풀어야 할지 모르겠다.
분명 이분탐색을 더 공부하고 싶어서 골랐지만...
경우의 수 문제는 그냥 해당 경우의 수를 구하는 방법밖에 생각이 나지 않았다.
풀이
경우의 수를 구해주는 풀이법
피자마다 각각 조합의 값이 몇개가 나오는지 count해주는 DP 배열을 만들었다.
피자의 조합의 경우의 수를 Count할 때, 몇가지 예외사항이 있다.
아무것도 선택하지 않는 경우는 1이며, 피자 전체를 선택하는 경우도 1이여야 한다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
public static void main(String[] args) throws IOException {
// 1.입력 -----
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int k = Integer.parseInt(br.readLine()); // 구하고자 하는 값
String[] x = br.readLine().split(" ");
int m = Integer.parseInt(x[0]);
int n = Integer.parseInt(x[1]);
int[] arrA = new int[m];
int[] arrB = new int[n];
int sumA = 0;
int sumB = 0;
for (int i = 0; i < m; i++) {
arrA[i] = Integer.parseInt(br.readLine());
sumA +=arrA[i];
}
for (int i = 0; i < n; i++) {
arrB[i] = Integer.parseInt(br.readLine());
sumB +=arrB[i];
}
// 2. 경우의 수 count -----
int[] DP1 = new int[k+1];
int[] DP2 = new int[k+1];
// 아무것도 선택 안하는 경우는 1번
DP1[0] = 1;
DP2[0] = 1;
// 개수 count
count_pieces(DP1,arrA,k);
count_pieces(DP2,arrB,k);
// 전체 다 선택하는 경우도 1번
// 피자 모두를 선택하는값이 배열 범위를 초과했으면 그냥 0번으로 변경
sumA = sumA > k ? 0 : sumA;
sumB = sumB > k ? 0 : sumB;
DP1[sumA]=1;
DP2[sumB]=1;
// 3. 출력
int res=0;
for (int i = 0; i <= k; i++)
res += DP1[i] * DP2[k-i];
System.out.println(res);
br.close();
}
static void count_pieces(int[] DP, int[] arr, int k){
int len = arr.length;
for (int i = 0; i < len; i++) {
int sum = 0;
for (int j = 0; j < len-1; j++) { // 맨끝까지 돌지 말것, 어차피 전체선택은 1이니 따로 셋팅할거임
if(arr[(i+j)%len] + sum > k)
break;
sum += arr[(i+j)%len];
DP[sum]++;
}
}
}
}DP 배열을 0 ~ k (구하고자하는 합) 까지로 선언해서
해당 값을 만들수 있는 경우의 수를 Count해서 넣어주어
A,B 각각의 합이 k가 되는 경우의 수를 곱해주는 경우를 다 더해주면 된다.
조금 지저분해 보이는건 나만 그런게 아니겠지...
경우의 수로 푸는것도 전체선택에 대한 예외사항들 때문에 오래걸렸다.
사실 이 문제는 이분탐색으로 푸는 문제이니, 이분탐색 풀이도 살펴보자
풀이 (이분탐색)
import java.util.ArrayList;
import java.util.Collections;
import java.util.Scanner;
public class Main {
static int target;
static int m;
static int n;
static int[] A;
static int[] B;
static boolean[] check;
static ArrayList<Integer> AList = new ArrayList<>();
static ArrayList<Integer> BList = new ArrayList<>();
static int ans=0;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
target = sc.nextInt();
m = sc.nextInt();
n = sc.nextInt();
A=new int[m];
B=new int[n];
for (int i = 0; i <m ; i++) {
A[i] = sc.nextInt();
}
for (int i = 0; i <n ; i++) {
B[i] = sc.nextInt();
}
//A 피자에 대한 부분합 만들기
for (int i = 0; i <m ; i++) {
check = new boolean[m];
check[i]=true;
getSum(A[i], i, i+1, check, A, AList);
}
//B 피자에 대한 부분합 만들기
for (int i = 0; i <n ; i++) {
check = new boolean[n];
check[i]=true;
getSum(B[i], i, i+1, check, B, BList);
}
AList.add(0);
BList.add(0);
Collections.sort(AList);
Collections.sort(BList);
int leftIdx= 0;
int rightIdx = BList.size() -1;
while(leftIdx < AList.size() && rightIdx >=0){//두 배열 사이즈 안에서 실행
// left, right index의 value 가져옴.
int lv = AList.get(leftIdx);
int rv = BList.get(rightIdx);
if(lv+rv ==target){// 목표값이 등장했으므로
int lc =0;
int rc = 0;
while (leftIdx < AList.size() && AList.get(leftIdx) == lv){
lc++;
leftIdx++;
}
while (rightIdx >=0 && BList.get(rightIdx) == rv){
rc++;
rightIdx--;
}
ans += lc*rc;
}
if(lv+rv > target) rightIdx--;
if(lv+rv < target) leftIdx++;
}
System.out.println(ans);
}
private static void getSum(int sum, int startIdx, int idx, boolean[] check, int[] arr, ArrayList<Integer> list) {
if(idx == arr.length){
idx = 0;
}
list.add(sum);
// 아직 안담은 피자 조건에대해서만 && 순환 방지함.
if(check[idx] == false && sum <= target && idx != startIdx-1){
check[idx] =true;
getSum(sum+arr[idx] , startIdx, idx +1, check, arr,list);
}else {
return;
}
}
}

이분탐색 풀이는 1020ms 로
경우의수 풀이가 184ms 이니 이 문제를 이분탐색으로 풀 이유는 없을것 같다.
'Algorithm > Weekly Solved' 카테고리의 다른 글
| [백준 1695] 팰린드롬 만들기 - Java 코드 (0) | 2022.05.06 |
|---|---|
| [백준 1780] 종이의 개수 - Java 코드 (분할정복) (0) | 2022.04.18 |
| [백준 1922] 네트워크 연결 - Java코드 (크루스칼) (0) | 2022.04.09 |
| [백준 1431] 시리얼 번호 (정렬) - Java코드 (0) | 2022.02.17 |
| [KAKAO 2021] 합승 택시 요금 - Java 코드 (Dijkstra) ★★★★ (0) | 2022.01.19 |



