정렬 알고리즘
정렬 알고리즘은 알고리즘 과목 중에서 기초적으로 반드시 알고 지나가야되는 파트입니다.
데이터를 정렬하는 방법이 다양하다.
다양한 정렬알고리즘 종류별 특징과 장단점이 있으며,
상황별로 각각 유리한 정렬알고리즘이 있으니 정리해보자.
정렬 알고리즘의 종류는 아래와 같다

모든 정렬이 다 유용하지 않고, 반드시 알아야할 개념과 자주 사용하는 정렬 알고리즘 위주로 정리하겠다.
저 중 중요한것은 O(n2)의 시간복잡도를 갖는 알고리즘 (버블정렬, 선택정렬, 삽입정렬) 들과
그보다 좀더 빠르고 효율적인 O(n logn)의 복잡도를 갖는 알고리즘 (병합정렬, 퀵정렬 , 트리정렬) 들이다.

1. O(n2)의 시간복잡도
버블정렬, 선택정렬, 삽입정렬 3가지가 존재한다. 한줄로 특징을 줄여보자면
버블정렬은 서로 붙은애들끼리 자리 바꾸기,
선택정렬은 비교할 애들중 최소값 찾기 ,
삽입정렬은 그냥 연결리스트일때 하나씩 연결해주기 라고 말할수 있을것 같다.
모두가 중첩반복문을 통해 정렬된다는 공통점을 지니며
중간에 우연치않게 정렬이 완성되어도 끝까지 반복문을 돌아야 종료되는 비효율적인 정렬방법이다.
1) 버블 정렬 (Bubble Sort)
배열의 크기만큼 반복 하되,
[ 0-1 ] , [ 1-2 ] , [ 2-3 ] . . . . . . [ (n-1)-n]
이런식으로 바로 그 다음 노드와 비교해가면서 큰값을 뒤로보내주며 Sort하는 형식이다.
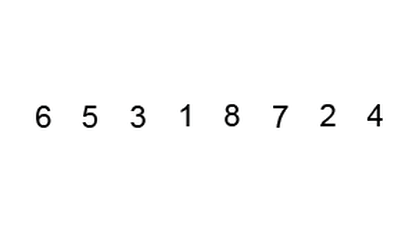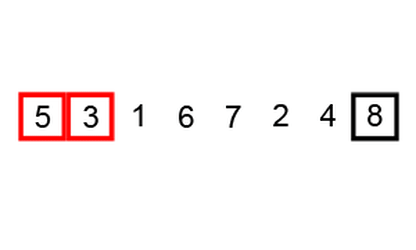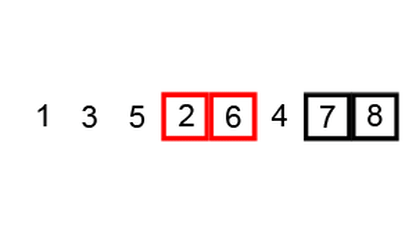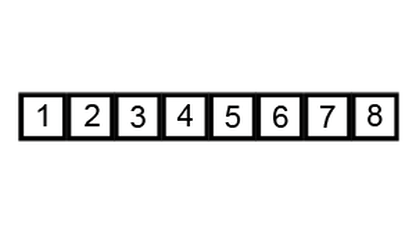
큰값하나가 뒤로가고 나머지 값들이 위로 한칸씩 올라가는 정렬이여서
여러 버블들이 보글보글 반복적으로 올라가는 것처럼 생각해서 버블소트이다.
(나는 공감 못함 큰값이 하나씩 뒤로갔는데? 드랍소트가 더 낫지 않나?)
public class SortMain {
public static void bubbleSort(int[] arr) {
final int length = arr.length;
for (int i = 0; i < length; i++) { // 배열의 길이만큼 도는데
for (int j = 0; j < length - i; j++) { // 0 ~ size -1까지
if (j + 1 < length && arr[j] > arr[j + 1]) { // 인접한 애들끼리 계속 비교하면서 자리교체
arr[j] = arr[j] + arr[j + 1];
arr[j + 1] = arr[j] - arr[j + 1];
arr[j] = arr[j] - arr[j + 1];
}
}
// 과정 출력
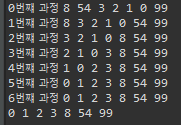
System.out.print(i+"번쨰 과정 ");
for(int x : arr)
System.out.print(x+" ");
System.out.println();
}
}
public static void main(String[] args) {
int[] arr = {8,54,99,3,2,1,0};
bubbleSort(arr);
for(int i : arr)
System.out.print(i+" ");
}
}
2) 선택 정렬 (Selection Sort)
선택정렬은 해당자리에 들어갈 최소값 or 최대값 (역순정렬시) 찾기라고 할 수 있다.
for문을 한번 돌때마다 한 자리가 완성되기 때문에,
기대값만큼만 정렬을 해줄수도 있다.
public static void selectionSort(int[] arr) {
final int length = arr.length;
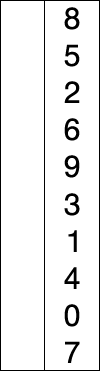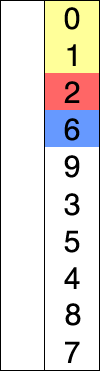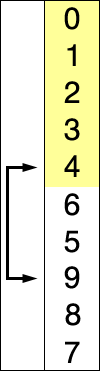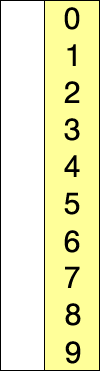
for (int i = 0; i < length; i++) {
int min = i;
for (int j = i + 1; j < length; j++) {
if (arr[j] < arr[min]) {
min = j;
}
}
// 나보다 작은게 있으면 치환
if (min != i) {
arr[min] = arr[min] + arr[i];
arr[i] = arr[min] - arr[i];
arr[min] = arr[min] - arr[i];
}
// 과정 출력
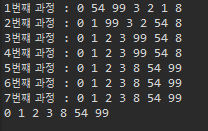
System.out.print((i+1)+"번쨰 과정 : ");
for(int x : arr)
System.out.print(x+" ");
System.out.println();
}
}
public static void main(String[] args) {
int[] arr = {8,54,99,3,2,1,0};
//bubbleSort(arr);
selectionSort(arr);
for(int i : arr)
System.out.print(i+" ");
}
3) 삽입 정렬 (Inertion Sort)
삽입정렬은 첫번째부터 도는 버블정렬이나, 선택정렬과는 조금 다른 성격을 지닌다.
두번째 인덱스부터 시작해서 자신의 앞에있는 값들과 비교하여 적절한 위치를 찾아 넣어주는 형식으로 진행된다.
즉, 정렬을 위해 비교하는 범위 자체가 훨씬 적고,
연산도 최소 O(n)만큼만 발생할 수 있다.
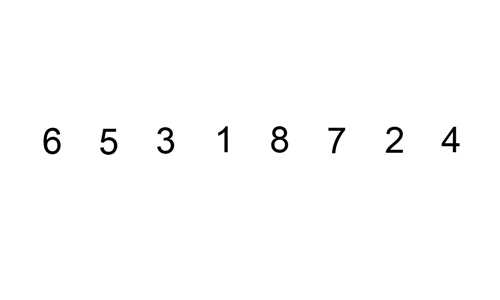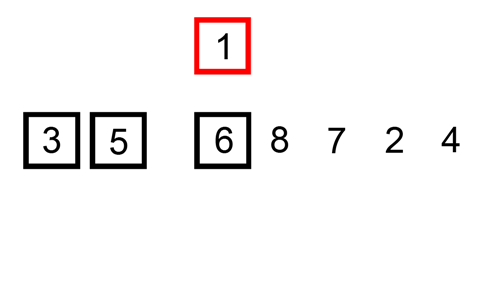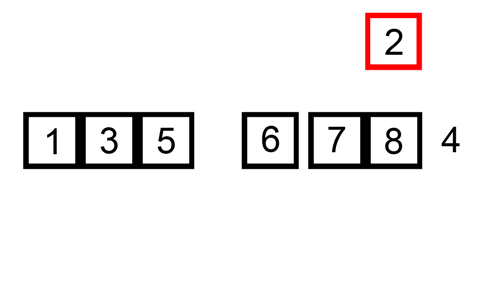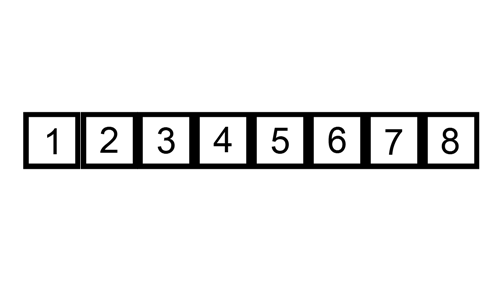
public static void insertionSort(int[] arr) {
// 정렬한 순서는 0번쨰가 아닌 1번째부터다
for (int i = 1; i < arr.length; i++) {
int key = arr[i];
int position = i;
// 자신의 바로 앞에 노드보다 값이 크기 전까지 뒤로 한칸씩 넣어줌
while (position > 0 && key < arr[position - 1]) {
arr[position] = arr[position - 1];
position--;
}
arr[position] = key;
// 과정 출력
System.out.print(i+"번째 과정 : ");
for(int x : arr)
System.out.print(x+" ");
System.out.println();
}
}

이미 정렬되어 있는 경우에는
앞에 노드보다 큰지 한번씩 밖에 비교를 하지 않아
시간 복잡도는 O(n)까지 줄게된다.
2. 성능
1). 시간복잡도
반복문을 도는 횟수는 Bubble = Selection >= Insertion 으로 얼마만큼 정렬되었는지가 삽입정렬이 반복 횟수와 연결된다.
| 정렬 알고리즘 | 최적의 경우 (오메가) | 평균적인 경우 (델타) | 최악의 경우 (빅오) |
| Bubble Sort | n^2 | n^2 | n^2 |
| Selection Sort | n^2 | n^2 | n^2 |
| Insertion Sort | n | n^2 | n^2 |
2). 비교연산
버블정렬은 (n-1)2 만큼 비교되지만
선택정렬은 한자리씩 정렬이 완성되어 (n-1)! 만큼 비교하므로 배열의 크기가 작을수록 비교를 조금만 하게 되어 유리하다.
삽입정렬도 (n-1)! 만큼 비교연산을 한다.
3). 치환연산
버블정렬과 삽입정렬은 계속적인 치환이 일어나므로 그닥 좋지 못하다.
선택정렬은 한자리씩 최소값을 찾기때문에, N번만큼의 연산만 일어나므로 버블보다 좋다.
정리
버블정렬과 선택정렬은 단순하고 직관적이며, 구현이 쉽지만, 비효율적이므로 잘 사용하지않는다.
삽입정렬은 정렬이 어느정도 되있는 경우에 최소한의 비교와 연산이 이루어지므로, 성능이 좋아 사용된다.
P.S
정렬 알고리즘별 수도코드를 정리한 곳이 있네요!
https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=deardiary11&logNo=220571744021
7가지 정렬 알고리즘 수도 코드로 한눈에 보기/
안녕하세요 ^^ DiDA 입니다 :) 선택정렬? 버블정렬? 한번 탁 들으면 촤라라락 쓸 줄 알아야 할텐데ㅋㅋ ...
blog.naver.com
'Algorithm > 알고리즘 정리' 카테고리의 다른 글
| [Combination]- Java코드 (DFS, BFS 방식 -성능비교) (0) | 2021.12.20 |
|---|---|
| 정렬 알고리즘 (2) - 퀵, 머지, 힙, JAVA 구현코드 (0) | 2021.07.08 |
| [알고리즘] 알고리즘별, 자료구조별, 시간복잡도 - 총정리 (0) | 2021.07.02 |
| [자료구조] Hash란? Java로 구현코드 (0) | 2021.06.07 |



