지난번 정렬 알고리즘중 O(n2)의 시간복잡도를 갖는 알고리즘 (버블정렬, 선택정렬, 삽입정렬) 을 정리해보았다.
정렬 알고리즘(1) - 버블, 선택, 삽입 , JAVA 구현코드
정렬 알고리즘 정렬 알고리즘은 알고리즘 과목 중에서 기초적으로 반드시 알고 지나가야되는 파트입니다. 데이터를 정렬하는 방법이 다양하다. 다양한 정렬알고리즘 종류별 특징과 장단점이
bangu4.tistory.com
이번에는 그 보다 좀 더 빠르고 효율적인 O(n logn)의 복잡도를 갖는 알고리즘 (병합정렬, 퀵정렬 , 트리정렬) 을 정리해보자.
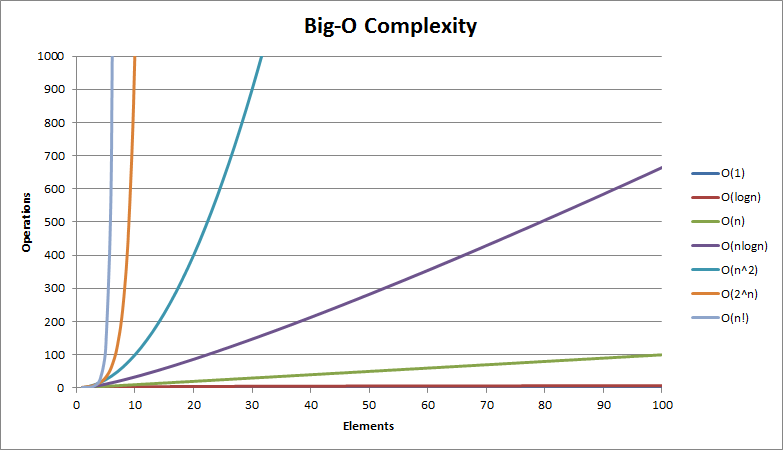
1. O(n logn)의 시간복잡도
퀵소트, 힙 소트, 머지소트 3가지가 존재한다.
모두 다 트리의 개념이 들어간 정렬 알고리즘이며,
퀵소트와 머지소트는 분할 정복 알고리즘이라고도 분류한다.
각각의 정렬 알고리즘을 한줄로 특징을 줄여보자면
퀵소트 피봇을 기준으로 작은값은 앞으로, 큰값은 뒤로 재귀적으로 분할정복 정렬
힙 소트 힙을 이용한 정렬?
머지소트 분할정복이라나 뭐라나?
1) 퀵 정렬
퀵소트는 재귀호출을 하는 분할정복 알고리즘으로
중간지점을 기준 삼아 중간지점의 값을 기준 (피봇)으로 삼아
작은값은 앞쪽, 큰값는 뒤쪽에 위치하도록 서로 자리를 바꾼다. (정복)
해당과정이 끝날때 큰값으로 정렬된 쪽에 첫번째 인덱스를 알 수 있다.
해당값을 이용해 두 파트로 범위를 나누어 또 다시 모두 퀵소트를 수행한다.
그렇게 섹션을 나눠가면서 새로운 피봇을 기준으로 정렬하는 퀵소트 과정을 반복하다보면,
결국 마지막섹션은 자신의 올바른 위치를 가지는 하나의 노드만 남게되므로
전체 배열이 완전히 정렬된 상태를 가지게 된다.
* 정말 많은 블로그 글을 읽었지만,
제대로 이해시켜주는 글은 없었습니다.
코드를 돌려봐도 이해되지 않았습니다,
개념을 흔드는 잘못된 정리글도 많습니다.
아래 유튜버분의 정리 영상은 아주 깔끔하고 명확하게 개념을 정리해주어. 확실하게 이해가 됩니다.
저 또한 퀵소트에 대한 많은 글보다 그냥 아래 영상을 따라 코딩해보시면서
한 두번 돌려보시면서 이해하시는게 더 좋을것같다고 생각하여 링크 남깁니다.
https://www.youtube.com/watch?v=7BDzle2n47c
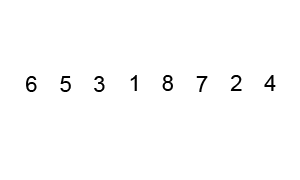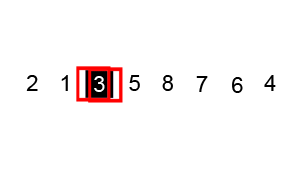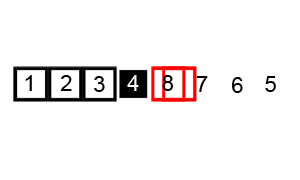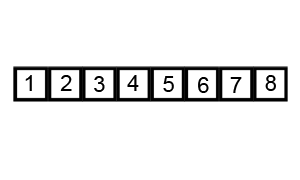
아래 코드가 길어보이지만, 오히려 함수화 되어있기때문에 이해하기 쉬울것이라 생각합니다.
public static void main(String[] args) {
int[] arr = {11,4,8,5,9,21,7,15,1,13};
quickSort(arr, 0, arr.length - 1);
for (int i : arr)
System.out.print(i+ " ");
System.out.println(" - 최종 결과");
}
// 퀵소트는 재귀적으로 호출되며, 두 파티션으로 쪼개가면서 정렬을 하는 분할정복 알고리즘이다.
public static void quickSort(int[] arr, int start, int end) {
// 소팅후 정렬이 완료된 시점에 두 섹션을 나누는 뒤쪽 시작점을 반환
int part2 = partion(arr,start,end);
// 앞쪽 파트 소팅
if(start < part2-1)
quickSort(arr, start, part2-1);
// 뒤쪽 파트 소팅
if(part2 < end)
quickSort(arr,part2, end);
}
// 정렬후 나눠지는 두배열중 뒤쪽 배열의 시작점을 반환
public static int partion(int[] arr, int start, int end) {
printProcess(arr);
int pivot = arr[(start+end)/2];
System.out.println(" -- s,p,e : " +start +" "+(start+end)/2+" "+end + " - pivot="+pivot);
while(start<=end) { // 피봇값을 기준으로 큰값은 왼쪽 작은값은 오른쪽 정렬됨
while(arr[start] < pivot) start++; // 왼쪽 파티션 순회하면서 피봇값과 같거나 큰 경우 swap을 위해 멈춤
while(arr[end] > pivot) end--; // 오른쪽 파티션 순회하면서 피봇값과 같거나 작은 경우 swap을 위해 멈춤
if(start<=end) { // 서로가 교차되지 않은 경우만 swap
swap(arr,start,end);
start++;
end--;
}// 서로가 교차된 경우 swap하지 않고 정렬이 다 된 상태일것
}
return start;
}
public static void printProcess(int[] arr) {
for(int i : arr)
System.out.print(i+" ");
}
public static void swap(int[] arr, int a, int b){
int tmp = arr[a];
arr[a] = arr[b];
arr[b] = tmp;
}
퀵소트의 시간복잡도는 최소 O(n logn) ~ O(n2)이지만, n2이 나올 확률은 현저히 낮다.
중간지 피봇값을 잡을때마다 최솟값만을 처음부터 끝까지 잡게되어야 O(n2)을 가진다.
실제 수행에서는 O(n logn) 보다 훨씬 성능이 좋다고 말한다.
(힙 , 병합정렬보다 20%이상 효율적이라고 함)
2) 병합정렬
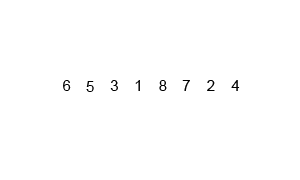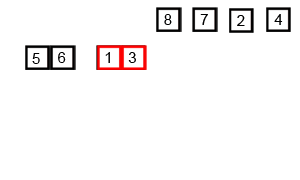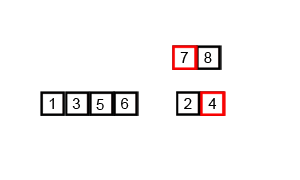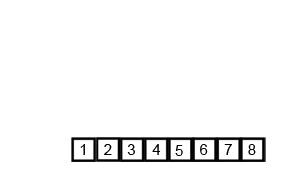
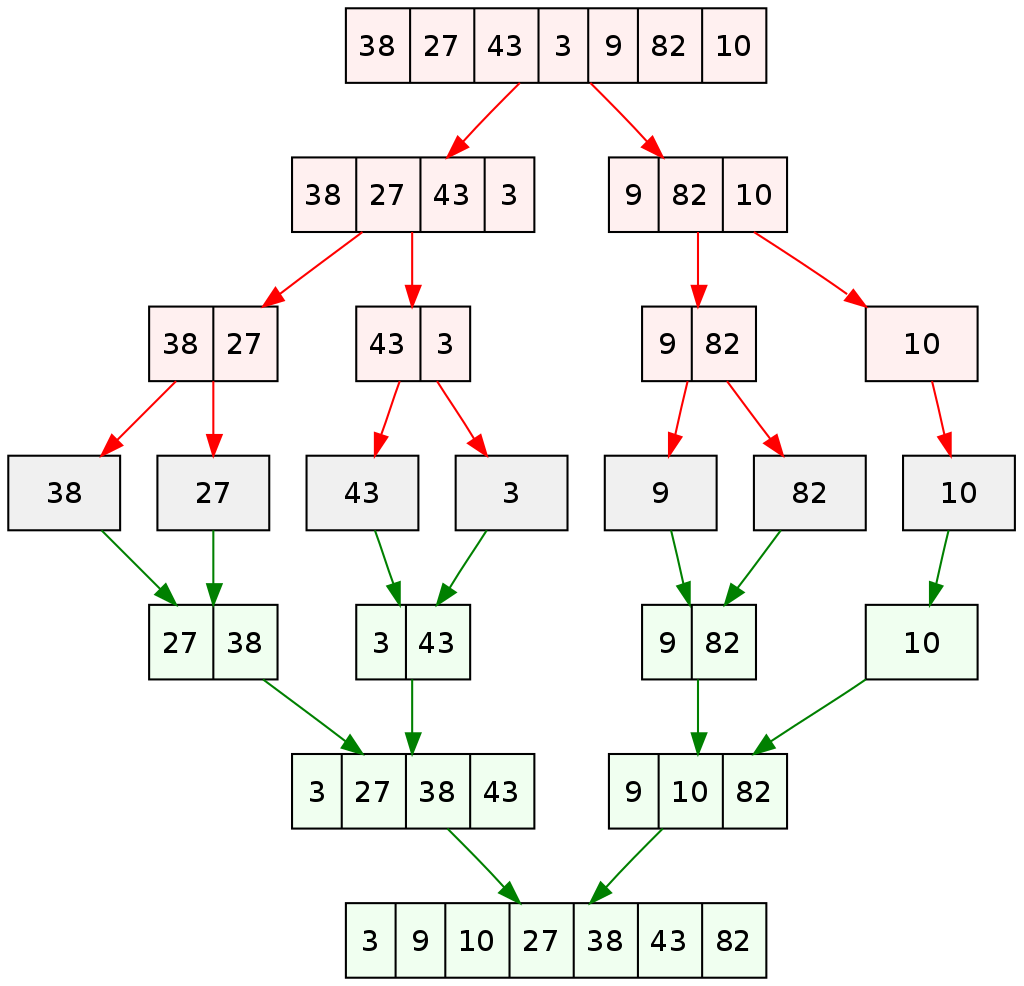
병합 정렬(merge sort) 알고리즘의 개념 요약
리스트의 길이가 0 또는 1이면 이미 정렬된 것으로 본다.
그렇지 않은 경우에는 정렬되지 않은 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눈다.
각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬한다. 두 부분 리스트를 다시 하나의 정렬된 리스트로 합병한다.
합병 정렬(merge sort) 알고리즘의 구체적인 개념
하나의 리스트를 두 개의 균등한 크기로 분할하고 분할된 부분 리스트를 정렬한 다음, 두 개의 정렬된 부분 리스트를 합하여 전체가 정렬된 리스트가 되게 하는 방법이다.
병합정렬은 다음의 단계들로 이루어진다.
병합(Divide): 입력 배열을 같은 크기의 2개의 부분 배열로 분할한다.
정복(Conquer): 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출 을 이용하여 다시 분할 정복 방법을 적용한다.
결합(Combine): 정렬된 부분 배열들을 하나의 배열에 합병한다.
병합 정렬의 과정
추가적인 리스트가 필요하다.
각 부분 배열을 정렬할 때도 합병 정렬을 순환적으로 호출하여 적용한다.
합병 정렬에서 실제로 정렬이 이루어지는 시점은 2개의 리스트를 병합(merge)하는 단계 이다.
public class Main {
public static int[] src;
public static int[] tmp;
public static void main(String[] args) {
src = new int[]{1,9,8,5,4,2,3,7,6};
tmp = new int[src.length];
printArray(src);
mergeSort(0, src.length - 1);
printArray(src);
}
public static void mergeSort(int start, int end) {
if (start < end) {
int mid = (start + end) / 2;
mergeSort(start, mid);
mergeSort(mid + 1, end);
int p = start;
int q = mid + 1;
int idx = p;
while (p <= mid || q <= end) {
if (q > end || (p <= mid && src[p] < src[q])) {
tmp[idx ++] = src[p ++];
} else {
tmp[idx ++] = src[q ++];
}
}
for (int i = start; i <= end; i ++) {
src[i] = tmp[i];
}
}
}
public static void printArray(int[] a) {
for (int i = 0; i < a.length; i ++)
System.out.print(a[i] + " ");
System.out.println();
}
}
먼저, merge sort라는 함수의 formal parameter인 int start와 int end를 보자.
start는 merge sort를 진행할 배열의 시작 인덱스를 의미하고, end는 마지막으로 포함될 배열의 인덱스를 의미한다.
앞서 올린 그림처럼 binary tree 형태로 쪼개기 때문에 int mid라는 start와 end의 중간 지점을 저장한다.
그 이후, 실제 분할을 진행하는데 첫 분할은 시작점부터 중간점까지인 mergeSort(start, mid)가 되고, 두 번째 분할은 중간점 다음부터 끝점까지인 mergeSort(mid+1, end)가 된다.
그다음, int p와 int q에 두 분할의 첫 번째 원소의 인덱스를 저장한다.
이 값을 저장하는 이유는, 해당 인덱스의 값을 비교하여 어떤 원소를 참조할지 정하기 때문이다.
start는 항상 mid+1보다 작기 때문에, 분할의 저장 위치는 start 지점이 된다. 그래서 int idx는 p가 된다.
그리고, p가 mid이하거나 q가 end이하일 때 동작해야 한다. 미만이 아닌 이유는 원소의 개수가 1개일 때까지 쪼개기 때문이다. 그리고 동시에 종료가 되지 않을 수 있으니 두 경우를 &&으로 하지 않고 ||으로 하는 것에 주의하자.
첫 번째 분할에서 원소를 가져오는 경우는 다음과 같다.
1. 두 번째 분할의 원소를 이미 다 가져온 경우 (q> end)
2. 첫 번째 분할에서 가져오지 않은 원소가 있고, 첫번째 분할의 첫 원소 값이 두 번째 분할의 첫 원소 값보다 작은 경우
위 조건을 표현하면 다음과 같다.
1. q> end
2. p <=mid && src [p]<src [q]
두 조건 중 하나 이상 만족하면 첫 번째 분할에서 원소를 가져오므로 두 조건 사이에 or을 사용한다.
그래서 if 문이 if (q>end || (p <=mid && src [p]<src [q])) 이렇게 선언된 것이다.
if 문에 결과에 따라 1번 분할의 첫 번째 값이나, 2번 분할의 첫번째 값을 정렬된 값을 임시 저장하는 배열인 tmp의 idx에 저장해준다.
이때, 가져온 원소의 다음 인덱스를 다시 비교하기 위해 p++ 또는 q++를 조건에 맞게 해 준다.
( idx도 당연히 ++ 해줘야 한다. 그다음 최솟값을 찾아서 저장할 거니까 )
그리고, 1번 분할과 2번 분할의 모든 원소를 가져오면, start 부터 end까지 정렬된 값을 다시 src라는 원래 배열에 저장해준다.
3) 힙정렬

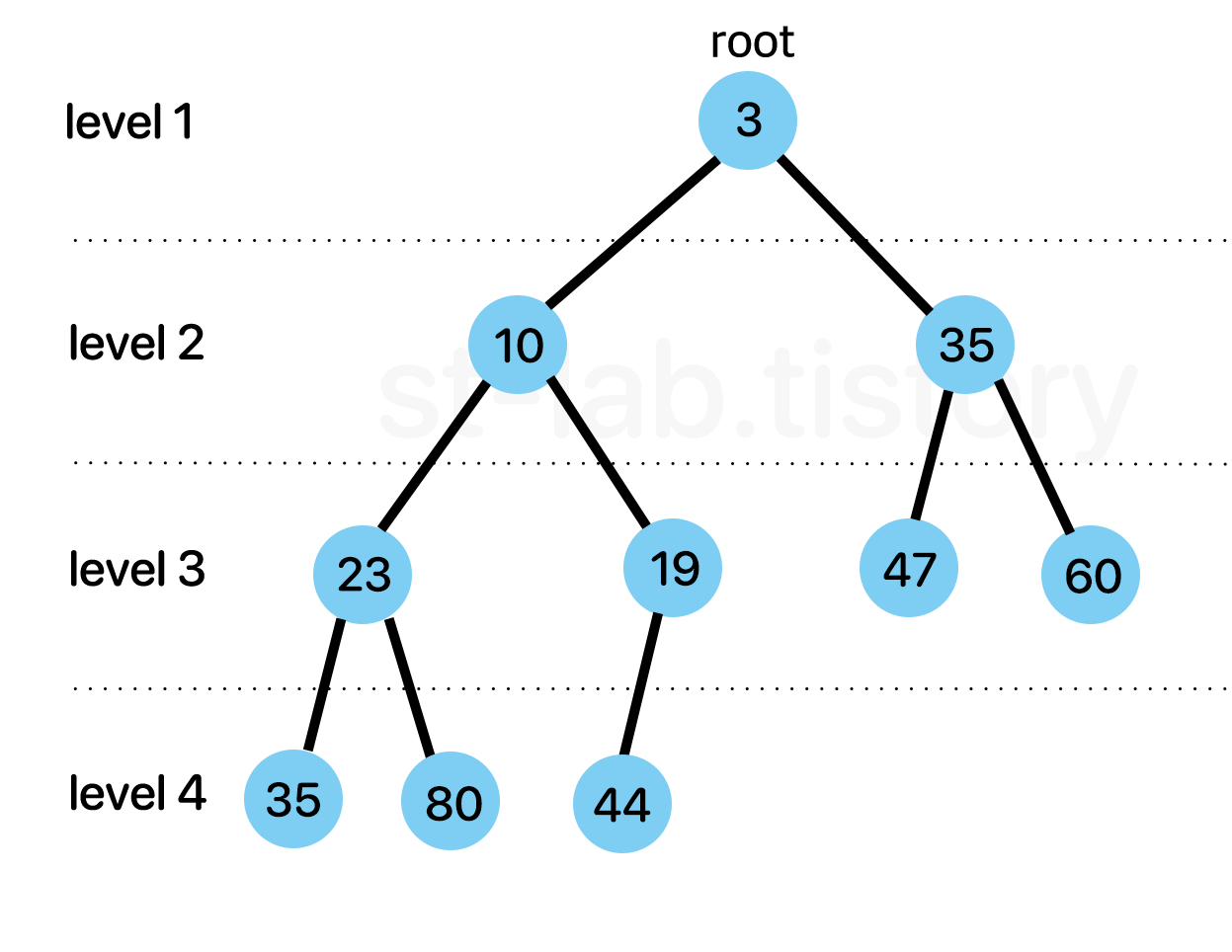
힙은 '최솟값 또는 최댓값을 빠르게 찾아내기 위해 완전이진트리 형태로 만들어진 자료구조'다.
위 문장에서 중요한 키워드 3가지가 있다. 바로 '최솟값 또는 최댓값' , '빠르게', '완전이진트리' 이다.
여러분이 어떤 리스트에 값을 넣었다가 빼낼려고 할 때, 우선순위가 높은 것 부터 빼내려고 한다면 대개 정렬을 떠올리게 된다.
쉽게 생각해서 숫자가 낮을 수록 우선순위가 높다고 가정할 때 매 번 새 원소가 들어올 때 마다 이미 리스트에 있던 원소들과 비교를 하고 정렬을 해야한다.
문제는 이렇게 하면 비효율적이기 때문에 좀 더 효율이 좋게 만들기 위하여 다음과 같은 조건을 붙였다.
'부모 노드는 항상 자식 노드보다 우선순위가 높다.'
즉, 모든 요소들을 고려하여 우선순위를 정할 필요 없이 부모 노드는 자식노드보다 항상 우선순위가 앞선다는 조건만 만족시키며 완전이진트리 형태로 채워나가는 것이다.
import java.util.PriorityQueue;
public class test {
public static void main(String[] args) {
int[] arr = {3, 7, 5, 4, 2, 8};
System.out.print(" 정렬 전 original 배열 : ");
for(int val : arr) {
System.out.print(val + " ");
}
PriorityQueue<Integer> heap = new PriorityQueue<Integer>();
// 배열을 힙으로 만든다.
for(int i = 0; i < arr.length; i++) {
heap.add(arr[i]);
}
// 힙에서 우선순위가 가장 높은 원소(root노드)를 하나씩 뽑는다.
for(int i = 0; i < arr.length; i++) {
arr[i] = heap.poll();
}
System.out.print("\n 정렬 후 배열 : ");
for(int val : arr) {
System.out.print(val + " ");
}
}
}
https://st-lab.tistory.com/225
자바 [JAVA] - 힙 정렬 (Heap Sort)
[정렬 알고리즘 모음] 더보기 1. 계수 정렬 (Counting Sort) 2. 선택 정렬 (Selection Sort) 3. 삽입 정렬 (Insertion Sort) 4. 거품 정렬 (Bubble Sort) 5. 셸 정렬 (Shell Sort) 6. 힙 정렬 (Heap Sort) - [현재..
st-lab.tistory.com
'Algorithm > 알고리즘 정리' 카테고리의 다른 글
| [Combination]- Java코드 (DFS, BFS 방식 -성능비교) (0) | 2021.12.20 |
|---|---|
| 정렬 알고리즘(1) - 버블, 선택, 삽입 , JAVA 구현코드 (2) | 2021.07.07 |
| [알고리즘] 알고리즘별, 자료구조별, 시간복잡도 - 총정리 (0) | 2021.07.02 |
| [자료구조] Hash란? Java로 구현코드 (0) | 2021.06.07 |



